仲のいい子としか組みたく無い生意気なガキ達を受け持った時にどうにか沢山二人組を作らせないといけない人向けの記事
ただしガキは友好関係を無向グラフで与えてくれるものとする(友好なのに無向)

マッチング
無向グラフに対して端点を共有しない辺集合
のこと
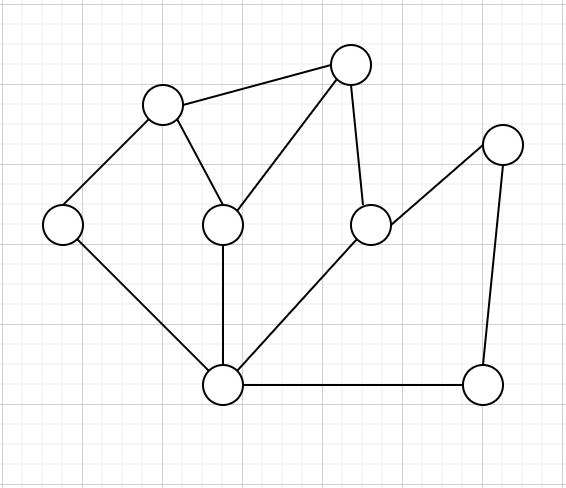

のうち最大のやつを求める方法を考える
頂点が
の辺の端点になってる時
は
にカバーされていると言う
今回の問題はカバーされてない頂点が最小となるマッチングを求めるとも言える
全ての頂点がカバーされてるマッチングのことを完全マッチングと言う

交互道
グラフ上の点素パスで、の辺と非
の辺を交互に使うやつ
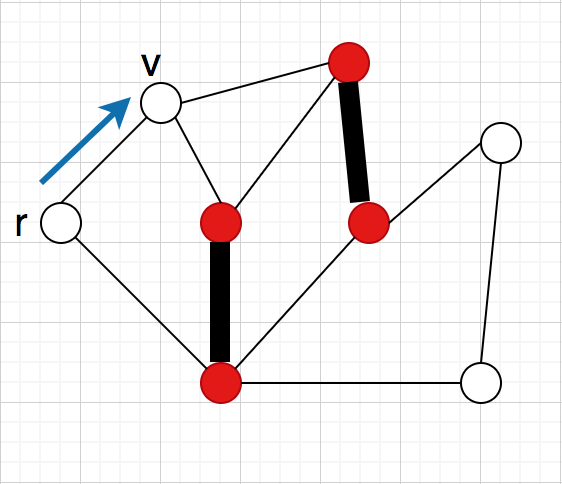
増加道
交互道で始点と終点がともにでカバーされてないやつ
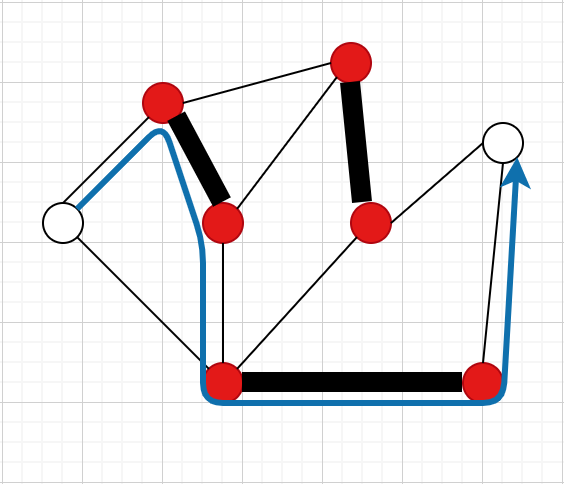
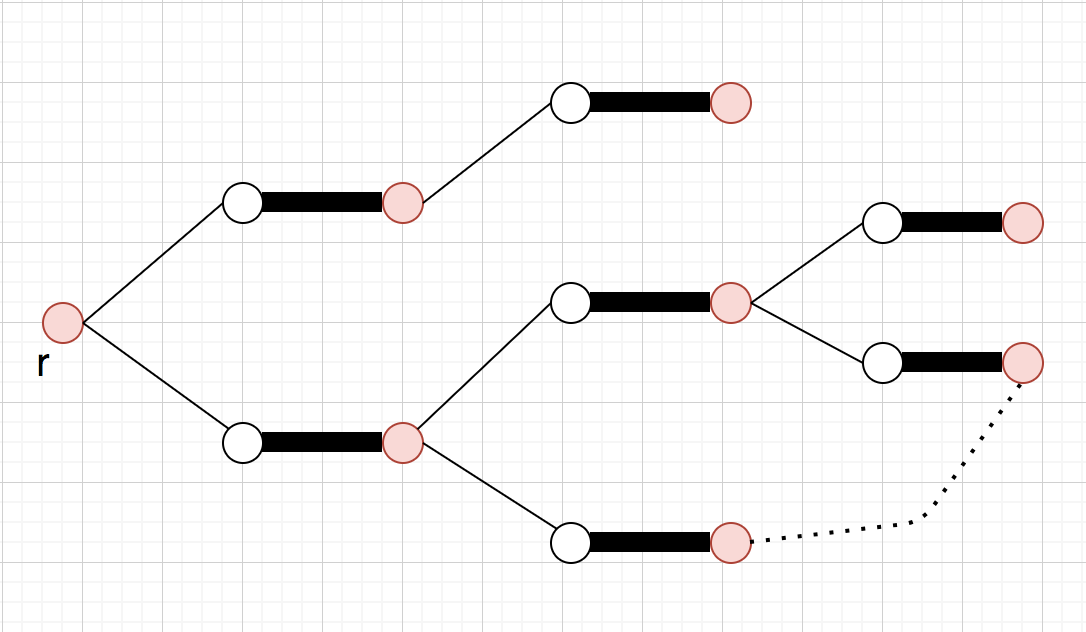
Thm
増加道があったらと増加道で対称差をとる(図のように
に入ってるかどうかを入れ替える)と一つサイズの大きいマッチングが出来る(この操作をaugmentと呼ぶ)
また、が最大マッチングで無い限り必ず増加道は存在する(
最大マッチング
と
の対称差をとると交互道と交互サイクルだけになることから示せる)


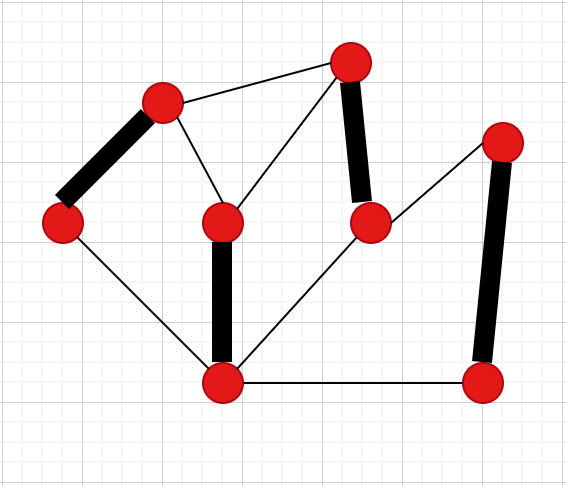
Thmより、最大マッチングになるまで増加道を見つけてすればOK
終わり
もうちょっとだけ続くんじゃ
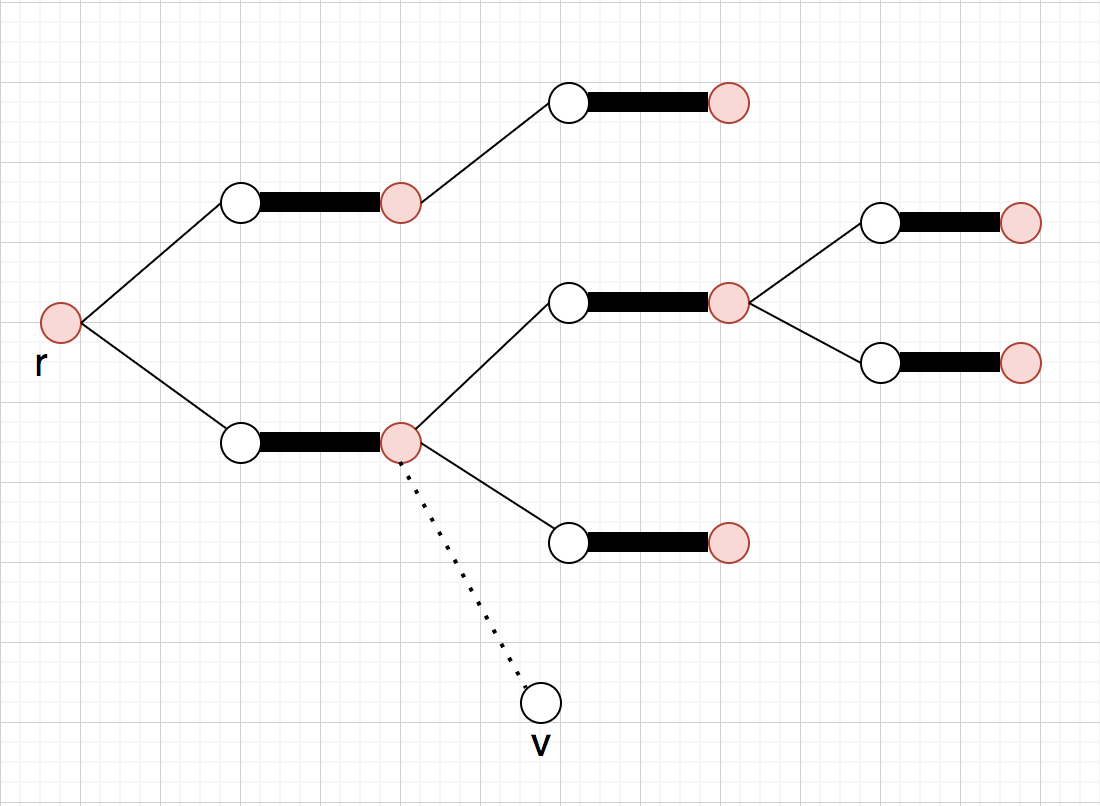
マッチングとカバーされてない頂点
が与えられた時、
(a)を始点とする増加道を見つけて
する
(b)をカバーしない最大マッチングが存在することを示し
をグラフから削除する
のどっちか片方を必ず行うアルゴリズムを作れれば、全ての点がカバーされたグラフになるまでこのアルゴリズムを適用することで最大マッチングが得られるのでこれを考える
が辺を持っていない時:明らかに
を削除していいのでOK
そうで無い時:
まずはを始点とする増加道を探す為、
を端点とする辺
を見る(この辺は当然
に含まれていない)
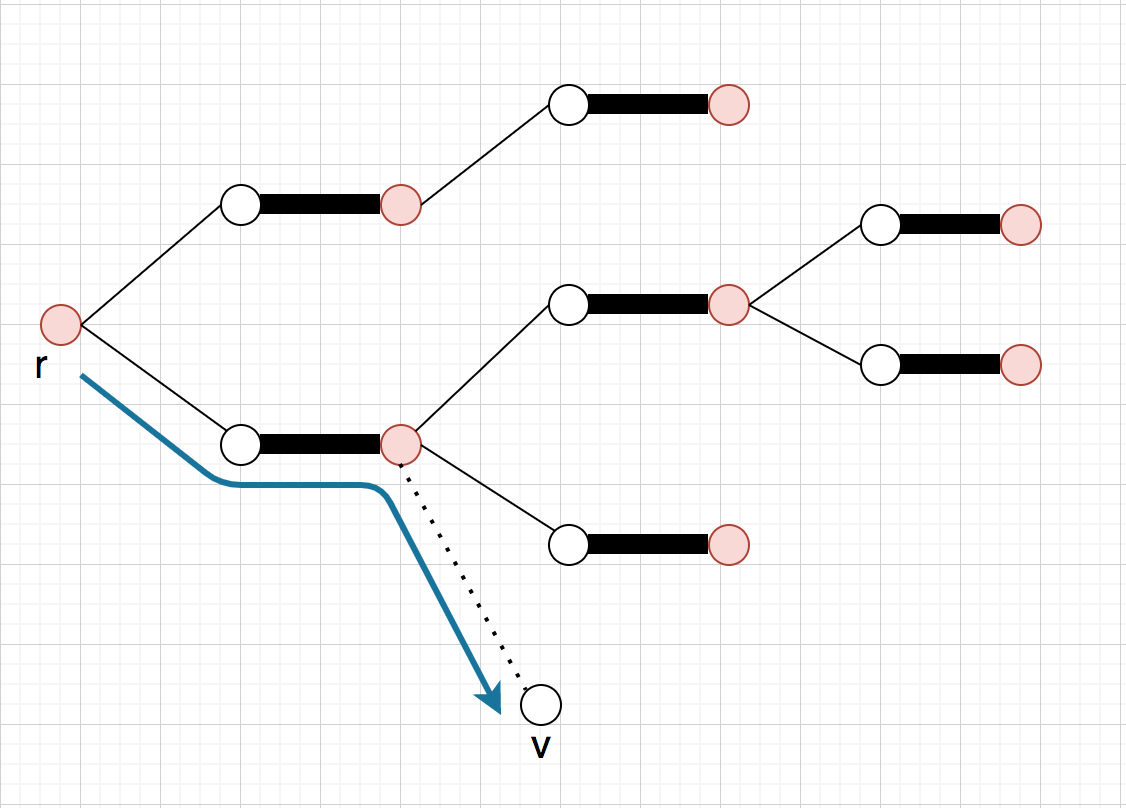
(A)がカバーされてない時:
増加道発見おめでとう
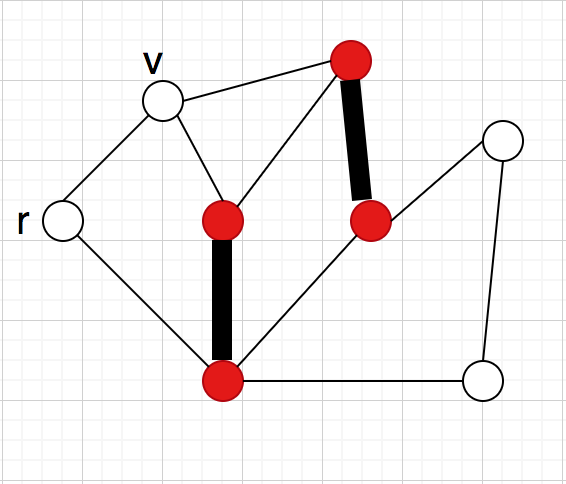
(B)が
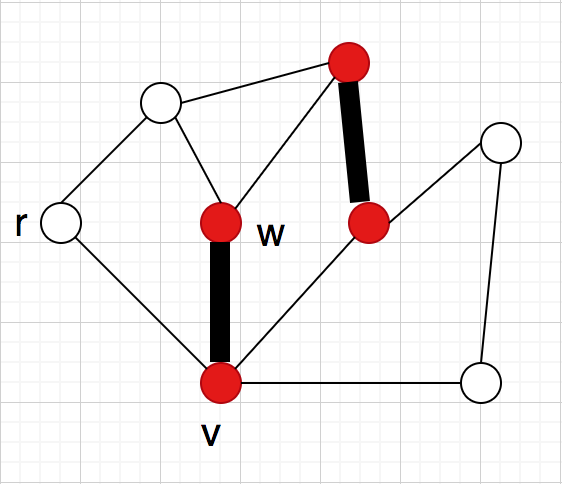
とマッチングしている時:
が交互道なので、
に隣接する非
辺も増加道の候補になる
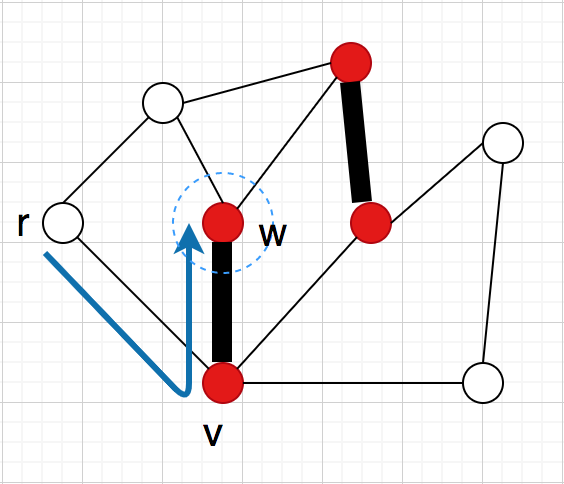
そこで、交互木と言うものを考えることにする
これはを根とする根付き木で、
の頂点は
のみカバーされていない
から
の各頂点への
上のパスは交互道になっている
の二つを満たすものである
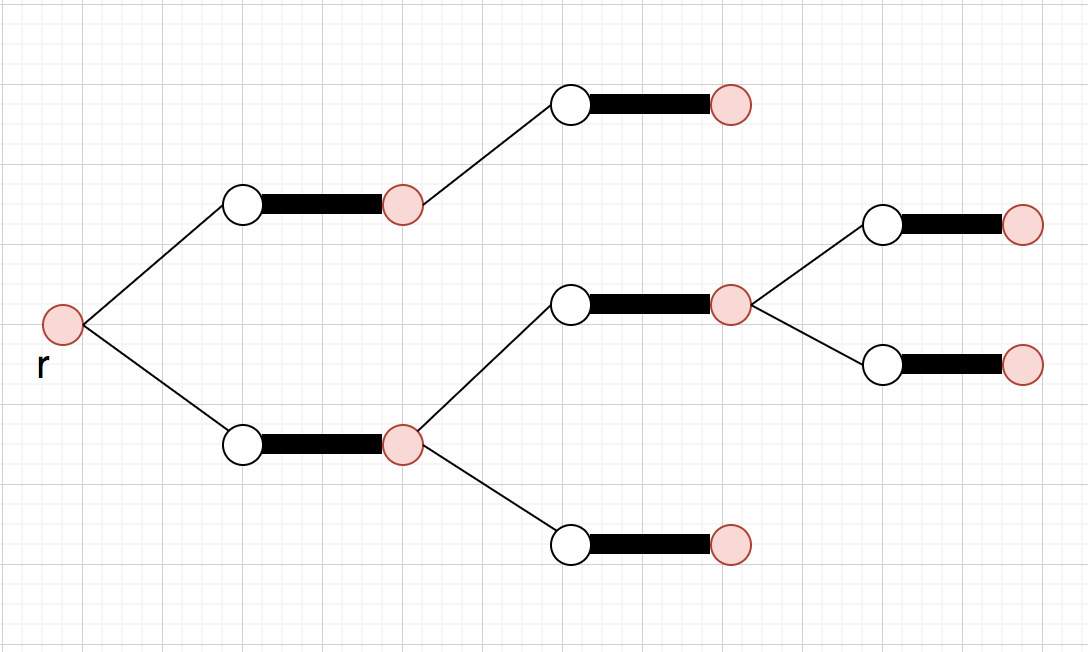
上の各頂点について、
からの
上の距離が偶数(奇数)の時偶点(奇点)と呼ぶ
この時、各偶点について、
外の頂点
に対し辺
が存在する時
(A')がカバーされてない時:
から
への増加道発見おめでとう
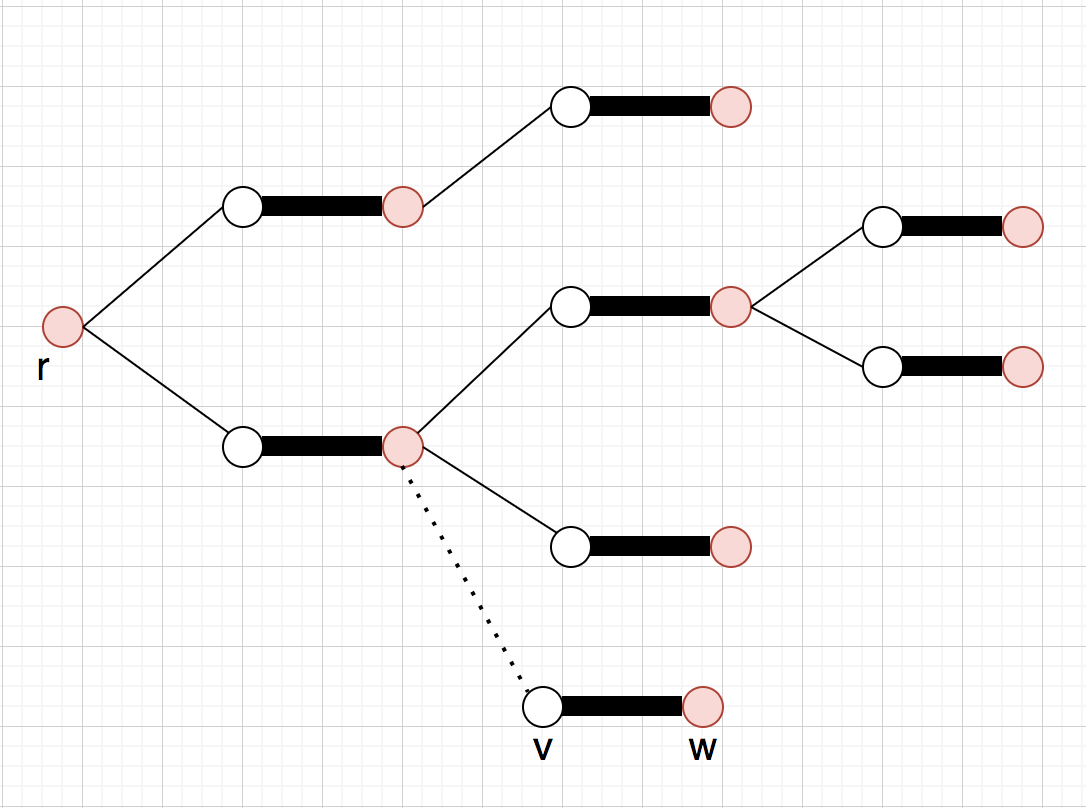
(B')が
とマッチングしている時(この時
は
の点では無い):
辺を
に加えて
を(交互木を保って)拡大出来る(この操作をextendと呼ぶ)
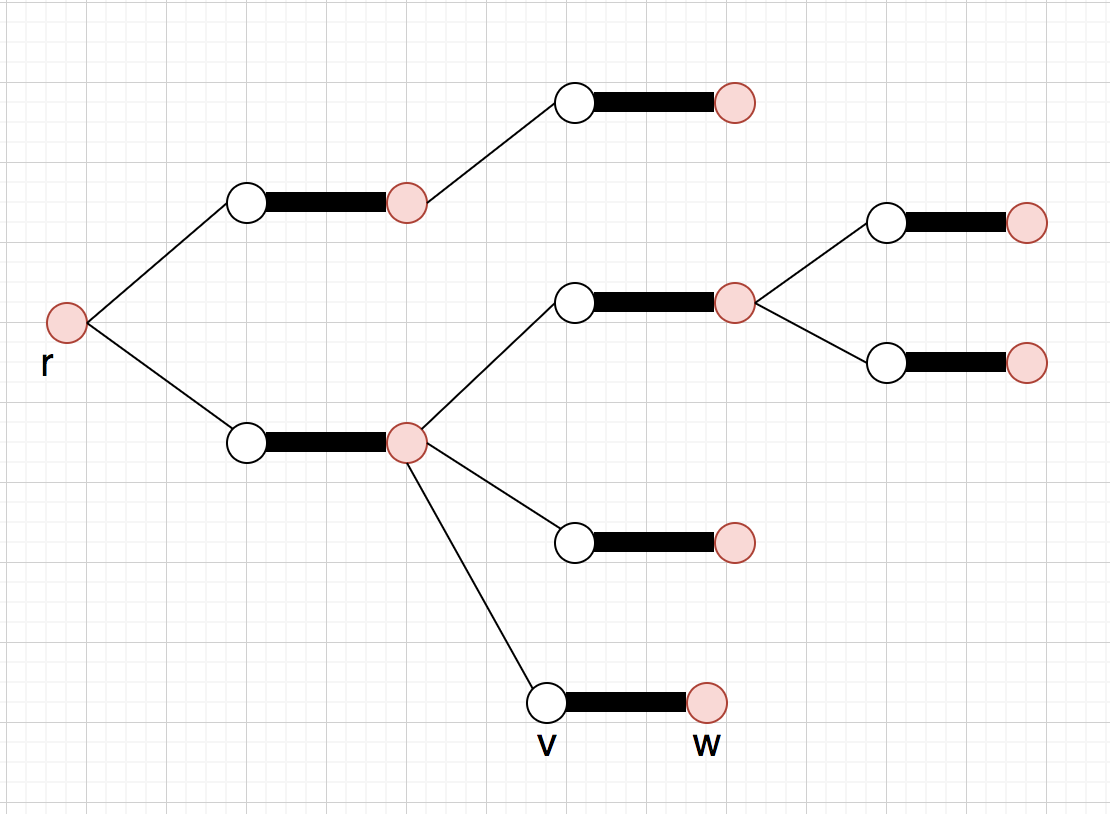
また、交互木には嬉しい性質が存在する
frustratedの定理(名前は適当)
交互木が、
の偶点を端点に持つような
の辺が全てもう片方の端点を
の奇点に持つ時frustratedと言う
この時、についてはマッチングを固定してしまい以降は
のみを考えることにして良い(この操作をdeleteと呼ぶ)
proof:
の奇点の数を
と置くと、偶点の数は
である(これは交互木なら常に成り立つ)
から奇点全部取り除くと、仮定から
個の偶点は全て孤立してしまう
この時、個の奇点と
個の偶点によるマッチングが存在するならそのマッチングを固定してしまって良い(偶点は奇点とマッチング出来なければ孤立してしまうため、奇点を偶点以外とマッチングさせることに嬉しさが無いので)
では実際
個の奇点と
個の偶点によるマッチングになっているから固定させてOK
進捗:
偶点から伸びてる辺の相手が全て奇点ならを削除出来る
偶点から伸びてる辺の相手がTの外のカバーされてない点ならaugment出来る
偶点から伸びてる辺の相手がTの外のカバーされている点ならextend出来る
未進捗:
偶点から伸びてる辺の相手が他の偶点の時
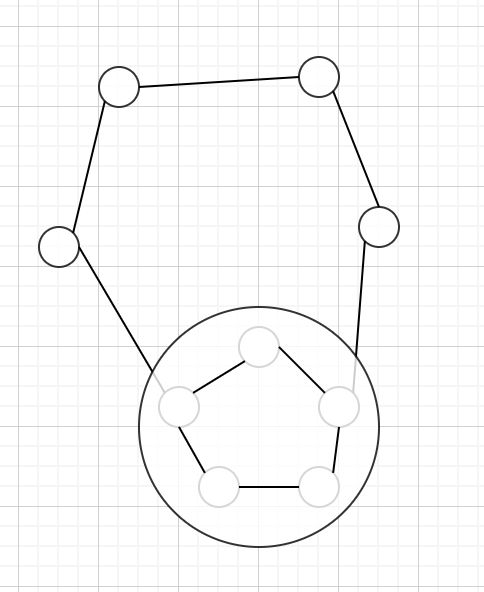
偶点から偶点に伸びてる辺が存在する時、図のように奇数長の閉路が出来る
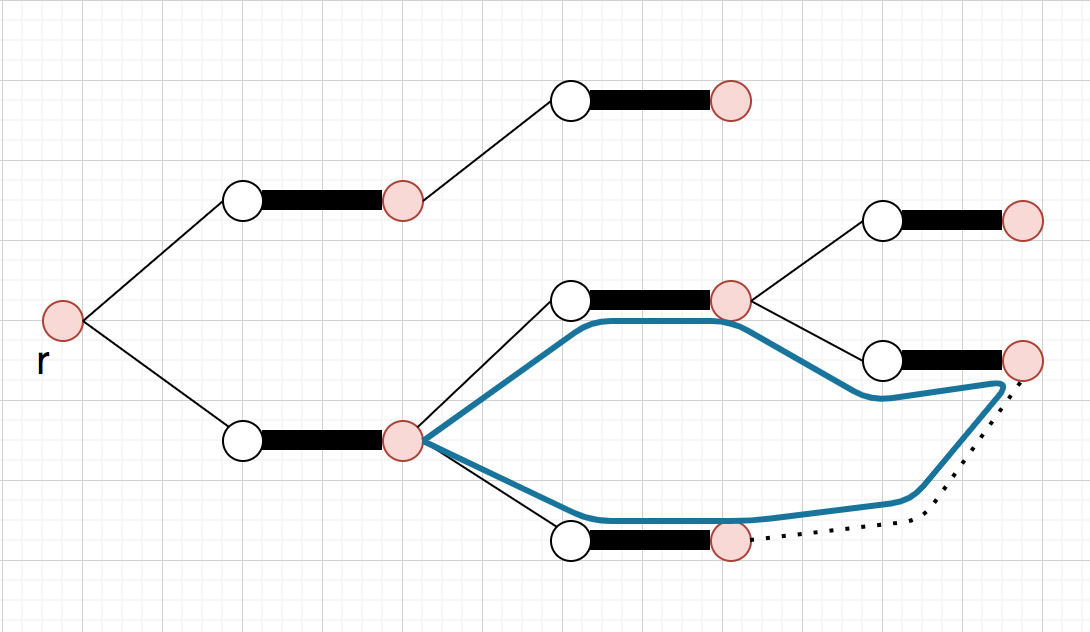
この時は、この閉路を図のように一点に縮約すると良いです(この操作をshrinkと言う)
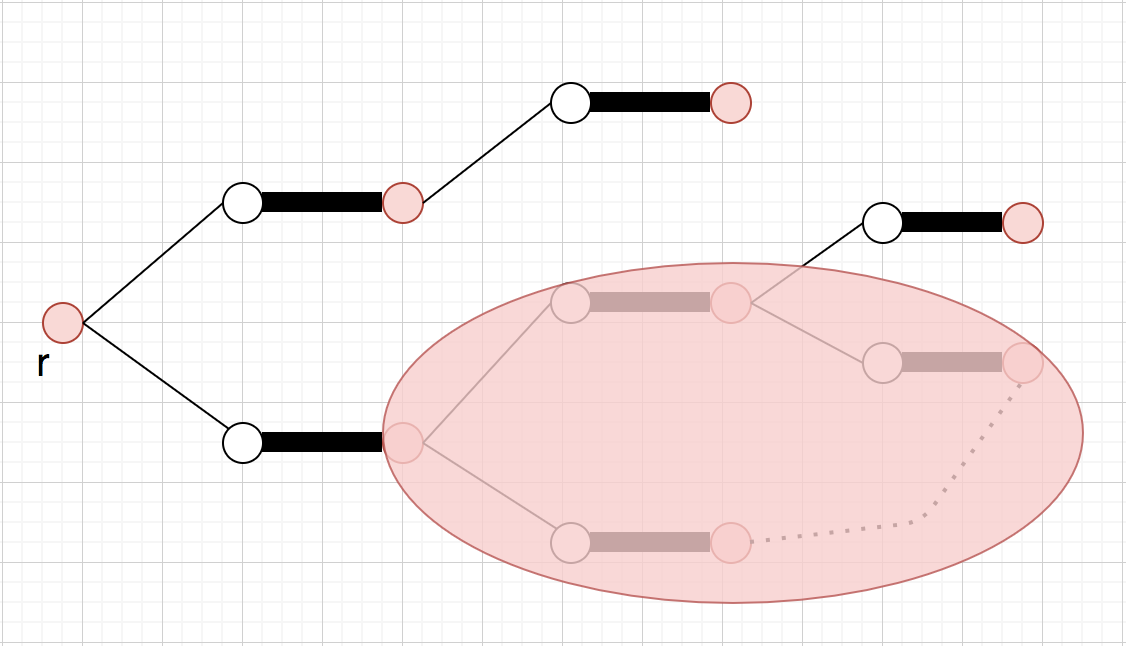
終わり
以下のことが成り立ちます
- 一点に潰す操作をしても交互木の性質を保つ
- 交互木の点のうち潰されて出来たものは全て偶点で、潰される前の頂点数は必ず奇数
- 任意の頂点は潰される前の世界で見ると因子臨界的
(頂点集合が因子臨界的:
からどの一点を除いても残りの
点で完全マッチングが出来る)
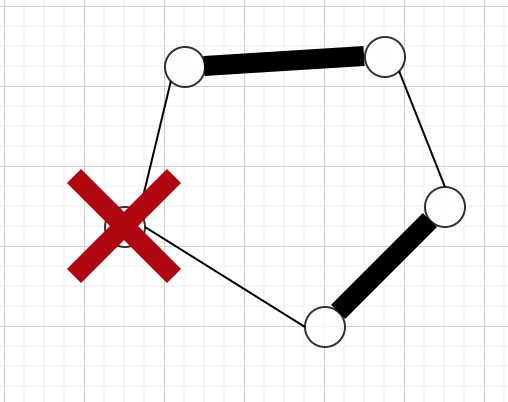
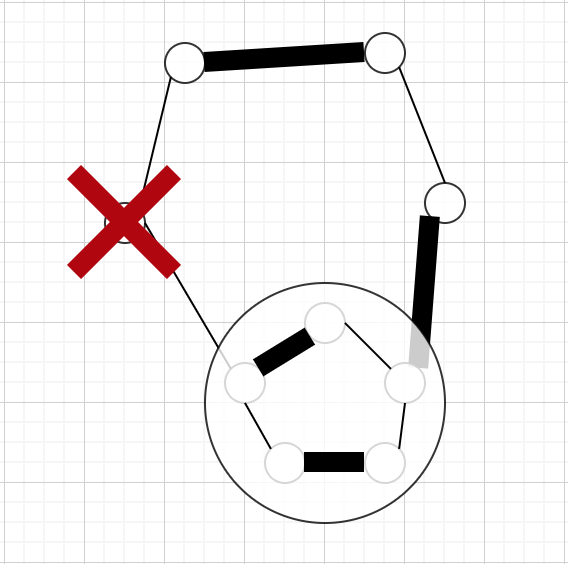
これらから、frustratedの定理は潰された頂点を含む場合にも適用して良いことがわかる
(個の奇点を除くと
個の 偶点=潰される前の世界における奇数連結成分 が孤立するから、奇点は各連結成分の一点とマッチングさせてやって良い。各連結成分は因子臨界的なので、一点が奇点とマッチングすれば残りの点は完全マッチングが作れる)
したがって、augmentかdeleteをするたびに潰されていた各点を引き戻してやり、引き戻す前とカバーされてない点の個数が変わらないようにいい感じにマッチングを張ってあげるとOK
分かりづらくなってきたのでアルゴリズムの形で書いてまとめる
グラフ,マッチング
,カバーされてない点
を与えるとaugmentかdeleteを必ず行う
Algoをカバーされてない点が全てdeleteされるまで繰り返すと最大マッチングになります
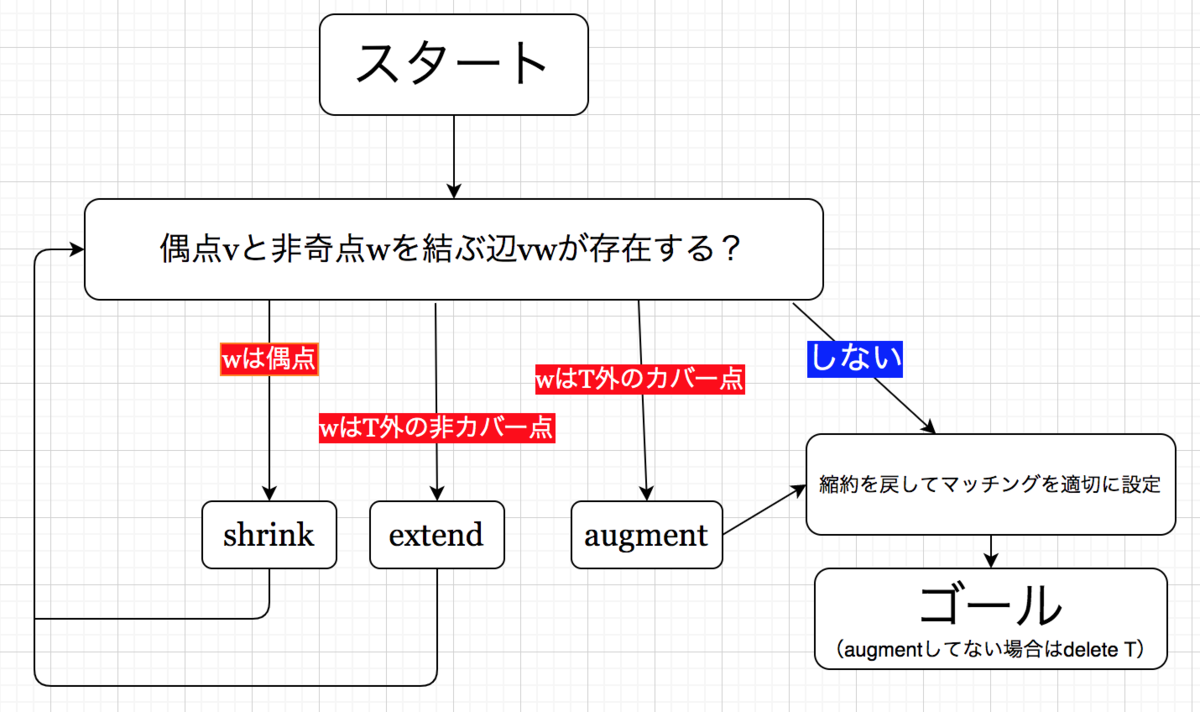
Algo
while:偶点vと非奇点wの間に辺が存在
if:wが偶点 )
else if wがカバーされてる: )
else
break;
shrinkを引き戻していい感じにマッチングを割り当てる
augmentして無い場合:
Algoは
- カバーされてない点の個数が増えることは無い
- while中頂点数が増えることは無い
- while中Tの外の点が増えることは無い
が成り立つから、
- 行われる回数は
(一回行うたびに考える必要のあるカバーされてない頂点数が減るので)
- 一回のAlgo中
の行われる回数は
(一回行うたびに頂点数が減るので)
- 一回のAlgo中
の行われる回数は
(一回行うたびに
の外の点が減るので)
したがって必ず停止する
計算量はの部分をうまくやると
とか使ってもほとんど変わらないはず
増加道を最短のものから見つける工夫をするとDinicの2部マッチングみたいにまで落ちるらしい
細かい実装とかは読者への演習問題とします
参考文献 : William J. Cook, William H. Cunningham, William R. Pulleyblank, Alexander Schrijver Combinatorial Optimization December 1997