E - Cigar Box

これの噛み砕き

$n=6,m=10,a=[2,1,3,6,5,4$ ]のケースを具体例にしつつ説明する
0-indexed で考える

最終的に「移動を経験する数の集合」は必ず「移動を経験しない集合」を左右から挟む形になる（集合は空かもしれないけど）
そこで、その「移動を経験する左右の集合」が左 $L$ 個、右 $R$ 個の時の場合を数えることにする
つまり、ソート列から $a$ の $[0,L)$ と $[n-R,n)$ は移動を経験、 $[L,n-R)$ は移動を経験せずに配置される
$a$ で $[L,n-R)$ が昇順に並んでない場合はソート列から $a$ を作るのが明らかに不可能なので、その時の場合の数は $0$

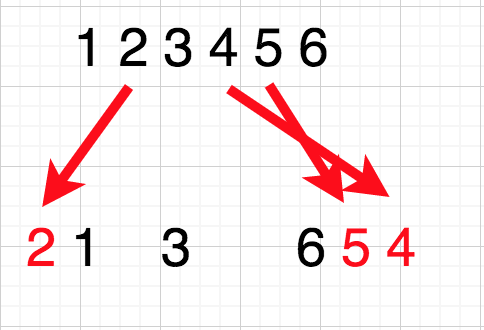
f:id:drogskol:20210214145556p:plain — (L,R)=(1,2)

この時は $1 3 6$ は動かさず、 $2 5 4$ だけを動かす

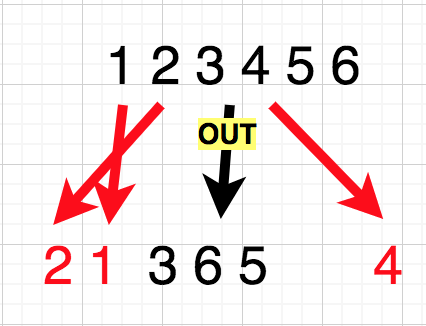
f:id:drogskol:20210214150006p:plain — (L,R)=(2,1)

こっちだと $3 6 5$ を動かさないこの時ソート済みの数列から $3 6 5$ の並びは作れないので数えない

次に移動 $m$ 個に役割を振り分ける
まず横一列に並んだ $m$ 個のボールで移動を表すことにし（左から $i$ 番目のボールが $i$ 回目の移動に対応）、ちょうど $L+R$ 個の空でないグループに分ける
※元記事では $L+R$ 色に塗り分けているけど実際には赤青赤と青赤青とかを区別しないので注意
同じグループのボールは同じ数を移動することに対応する

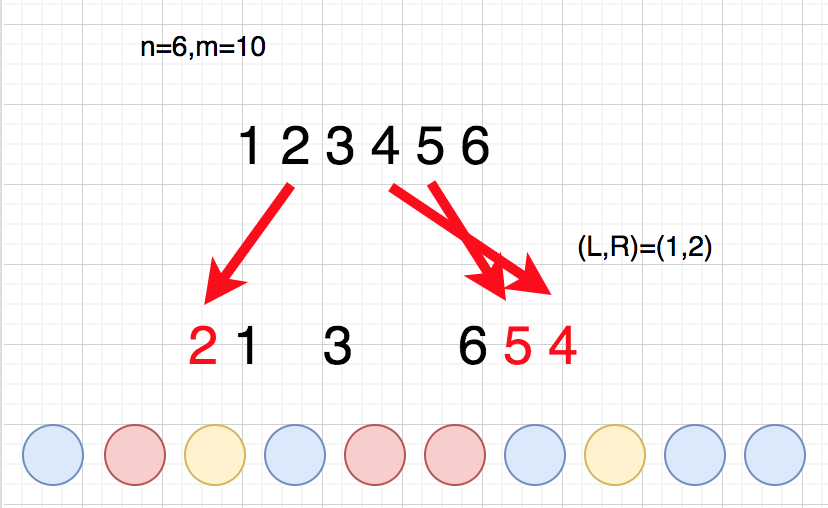
f:id:drogskol:20210214160423p:plain — m個のボールをL+R個のグループに分ける

$group [k$ ]で $k$ 個のグループに分ける通り数を表すことにすると、

$group [k ] = \dfrac{ k^m - \displaystyle\sum_{i=1}^{k-1} group [i ]{}_kP_i } {k!}$

と言う式で表すことが出来る
これは

$m$ 個のボールを $k$ 色で塗り分ける場合の数を数える
$i \lt k$ 色しか使ってないケースが $group[i]{}_kP_i$ だけ存在するので引く
（赤青赤と青赤青のように）同じグループを表す色ぬりが存在するので $k!$ で割る
と言う操作である

次に $L+R$ 種類のうち（その色の最後のボールが）左移動をする $L$ 個を決める

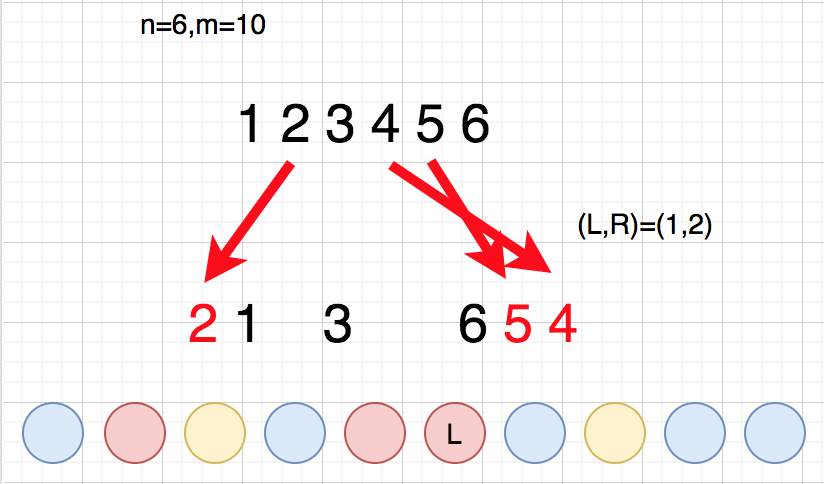
赤色の"最後の一個"が左移動を担当
こうすると自動的に各ボールがどの数を担当するかが決定する
例えば青と黄色は青の方が最後の一手が後ろにあるので、青が $a$ の右端の $4$ を担当

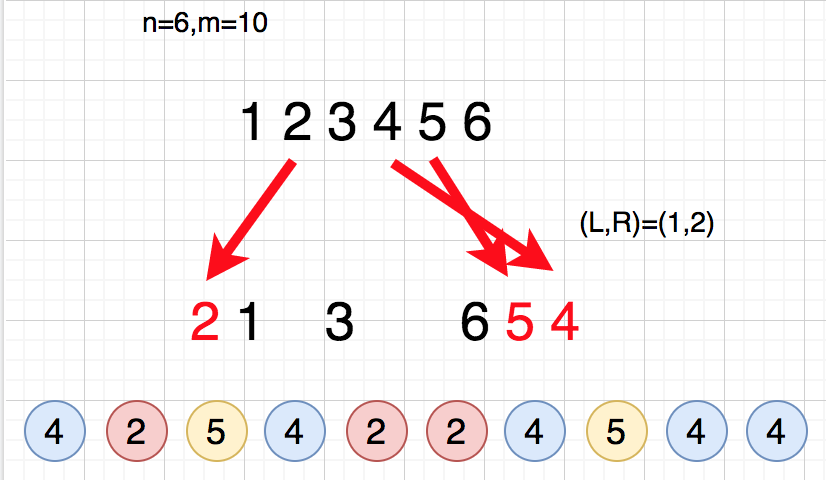
自動的に各グループの担当する数が決まる

各色について、最後の一手の左右は決まるがそれ以外については左右どちらを選んでも良い
最後の一手で無いボールは $m-(L+R)$ 個あるので、ここの向きの決め方が $2^{m-(L+R)}$ 通りである

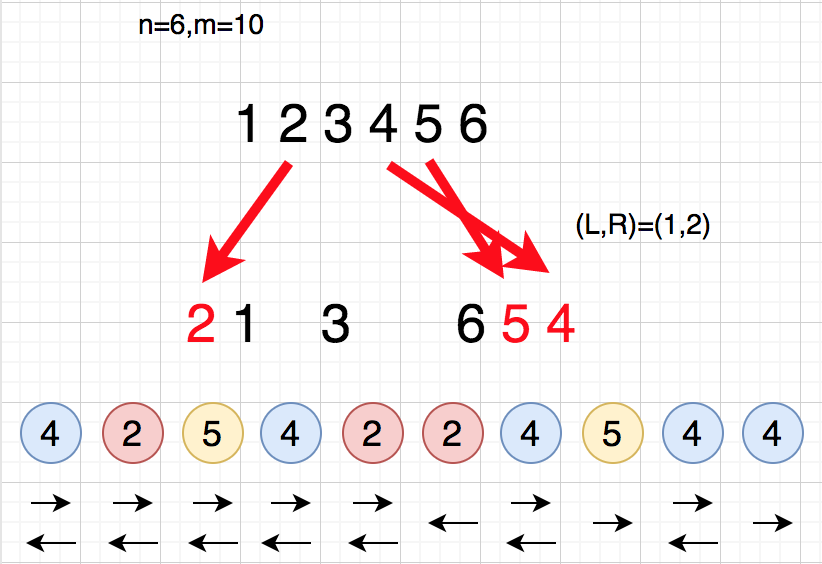
f:id:drogskol:20210214162020p:plain — 各グループ最後の一手のみ向きが固定されている

よって答えは
$\displaystyle \sum_{ \substack{1\leq L+R \leq m \\ L+R \leq n \\ a:[L,n-R)\text{昇順} } } group[L+R] \binom{L+R}{L} 2^{m-(L+R)}$

計算量は $A=max(n,m)$ とすると

$group$ を求めるのに $O(A^2)$
階乗や $2$ べきを前計算で求めておくのに $O(A)$
$(L,R)$ が $O(A^2)$ 個（各場合について移動しない区間が昇順かは $O(1)$ で求められる,下の実装参照）

よって全体で $O(A^2)$
以下の実装では $2$ べきの前計算をサボってるので $O(A^2 logA)$

#include<bits/stdc++.h>
#include<atcoder/modint>
using namespace std;
using mint=atcoder::modint998244353;

mint group[3001],Fact[3001],Finv[3001];//Fact[i]=i!,Finv[i]=1/(i!)
mint nCk(int n,int k){
  return Fact[n]*Finv[k]*Finv[n-k];
}

int main(){

  Fact[0]=Finv[0]=1;
  for(int i=1;i<=3000;i++){
    Fact[i]=Fact[i-1]*i;
    Finv[i]=Fact[i].inv();
  }

  int n,m;cin>>n>>m;
  vector<int> v(n);
  for(int &p:v)cin>>p;

  for(int k=1;k<=m;k++){
    group[k]=mint(k).pow(m);
    for(int i=1;i<k;i++)group[k]-=group[i]*Fact[k]*Finv[k-i];
    group[k]*=Finv[k];
  }

  mint ans=0;
  for(int l=0;l<=n;l++)//左にl個移動させる
    for(int j=l;j<=n;j++){//aの[j,n)は右移動によって持ってくる
      if(j-2>=l&&v[j-1]<v[j-2])break;//移動させない部分が昇順じゃない
      int r=n-j;
      if(m-l-r<0)continue;
      ans+=group[l+r]*nCk(l+r,l)*mint(2).pow(m-l-r);
    }
  cout<<ans.val()<<endl;
}

atcoder.jp

blogskol

思わず声に出して読みたくなるブログ

E - Cigar Box